Regression Coefficient
REGRESSION
Description also available in video format (attached
below), for better experience use your desktop.
Introduction
· Regression analysis
refers to assessing the relationship between the outcome variable and one or
more variables. The outcome variable is known as the dependent or response
variable and the risk elements, and
co-founders are known as predictors or independent variables. The
dependent variable is shown by “y” and independent variables are shown by “x”
in regression analysis.
· The sample of a correlation coefficient is estimated in
the correlation analysis. It ranges between -1 and +1, denoted by r and
quantifies the strength and direction of the linear association among two
variables. The correlation among two variables can either be positive, i.e. a
higher level of one variable is related to a higher level of another or
negative, i.e. a higher level of one variable is related to a lower level of
the other.
· The sign of the coefficient of correlation shows the
direction of the association. The magnitude of the coefficient shows the
strength of the association.
· For example, a correlation of r = 0.8 indicates a
positive and strong association among two variables, while a correlation of r =
-0.3 shows a negative and weak association. A correlation near to zero shows
the non-existence of linear association among two continuous variables.
Least
Square Method
·
The least square method is the
process of finding the best-fitting curve or line of best fit for a set of data
points by reducing the sum of the squares of the offsets (residual part) of the
points from the curve. During the process of finding the relation between two
variables, the trend of outcomes are estimated quantitatively. This process is
termed as regression analysis.
The method of curve fitting is an approach to regression analysis. This method
of fitting equations which approximates the curves to given raw data is the
least squares.
· It is quite obvious that the fitting of curves for a
particular data set are not always unique. Thus, it is required to find a curve
having a minimal deviation from all the measured data points. This is known as
the best-fitting curve and is found by using the least-squares method.
·
The least-squares method is a crucial statistical method that is practiced to find a regression line or a best-fit line for the given pattern.
This method is described by an equation with specific parameters. The method of
least squares is generously used in evaluation and regression. In regression
analysis, this method is said to be a standard approach for the approximation
of sets of equations having more equations than the number of unknowns.
· The method of least squares actually defines the solution for
the minimization of the sum of squares of deviations or the errors in the
result of each equation.
· The least-squares method is often applied in data fitting. The
best fit result is assumed to reduce the sum of squared errors or residuals
which are stated to be the differences between the observed or experimental
value and corresponding fitted value given in the model.
· There are two basic categories of least-squares problems:
- Ordinary or linear least squares
- Nonlinear least squares
· These depend upon linearity or nonlinearity of the residuals.
The linear problems are often seen in regression analysis in statistics. On the
other hand, the non-linear problems are generally used in the iterative method
of refinement in which the model is approximated to the linear one with each
iteration.
Least Square Method Formula
Least-square
method is the curve that best fits a set of observations with a minimum sum of
squared residuals or errors. Let us assume that the given points of data are (x1, y1), (x2, y2), (x3, y3), …, (xn, yn) in which all
x’s are independent variables, while all y’s are dependent ones. This method is
used to find a linear line of
the form y = mx + b, where y and x are variables, m is the slope, and b is the
y-intercept. The formula to calculate slope m and the value of b is given by:
m
= (n∑xy - ∑y∑x)/n∑x2 - (∑x)2
b
= (∑y - m∑x)/n
Here,
n is the number of data points.
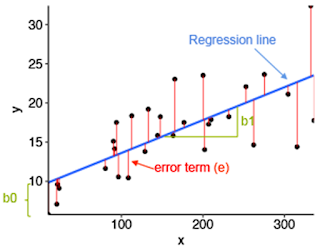
Least Square Method Graph
Look at the graph below, the straight line shows the
potential relationship between the independent variable and the dependent
variable. The ultimate goal of this method is to reduce this difference between
the observed response and the response predicted by the regression line. Less
residual means that the model fits better. The data points need to be minimized
by the method of reducing residuals of each point from the line. There are
vertical residuals and perpendicular residuals. Vertical is mostly used in
polynomials and hyperplane problems while perpendicular is used in general as
seen in the above image..
Method
of Regression Coefficient
Regression coefficients
can be defined as estimates of some unknown parameters to describe the
relationship between a predictor variable and the corresponding response. In
other words, regression coefficients are used to predict the value of an
unknown variable using a
known variable. Linear regression is used to quantify how a unit change in an
independent variable causes an effect in the dependent variable by determining
the equation of the best-fitted straight line. This process is known as regression analysis.
Formula for
Regression Coefficients
The
goal of linear regression is to find the equation of the straight line that
best describes the relationship between two or more variables. For example,
suppose a simple regression equation is given by y = 7x - 3, then 7 is the coeffiecient, x
is the predictor and -3 is the constant term. Suppose the equation of the
best-fitted line is given by Y = aX + b then, the regression coefficients
formula is given as follows:
Here, n refers to the number of
data points in the given data sets.
Regression Coefficients Graph
Properties
of regression coefficient
1. The regression coefficient is
denoted by b.
2. We express it in the form of
an original unit of data.
3. The regression coefficient of
y on x is denoted by byx.
The regression coefficient of x on y is denoted by bxy.
4. If one regression coefficient
is greater than 1, then the other will be less than 1.
5. They are not independent of
the change of scale. There will be change in the regression coefficient if x
and y are multiplied by any constant.
6. AM of both regression
coefficients is greater than or equal to the coefficient of correlation.
7. GM between the two regression
coefficients is equal to the correlation coefficient.
8. If bxy is
positive, then byx is also positive and vice versa.
Video
description
o Visit our Let’s contribute page https://keedainformation.blogspot.com/p/lets-contribute.html
o Follow our page
o Like & comment on our post

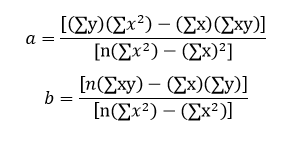




Comments